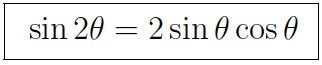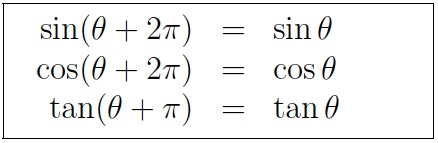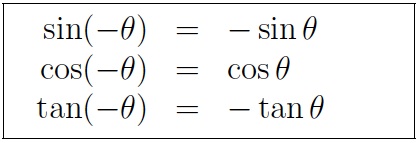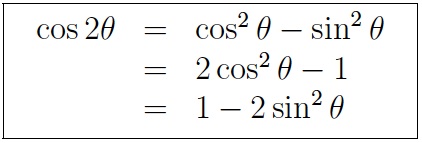Integration by Parts
Guidelines for selecting u and dv:
-
Remember “L-I-A-T-E” where you choose “u” to be the function that comes first in the list.
- L - Logrithmic Function
- I - Inverse Trig Function
- A - Algebraic Function
- T - Trig Function
- E - Exponential Function
- Example:

-
Alternative Guidelines for Choosing u and dv:
- dv is the complicated portion of the integrand that can easily be integrated.
- u is the integrand whose derivative du is a “simpler” function than u itself.
- Example:

-
Repeated Applications of Integration by Parts:

Trig Formulas to Memorize
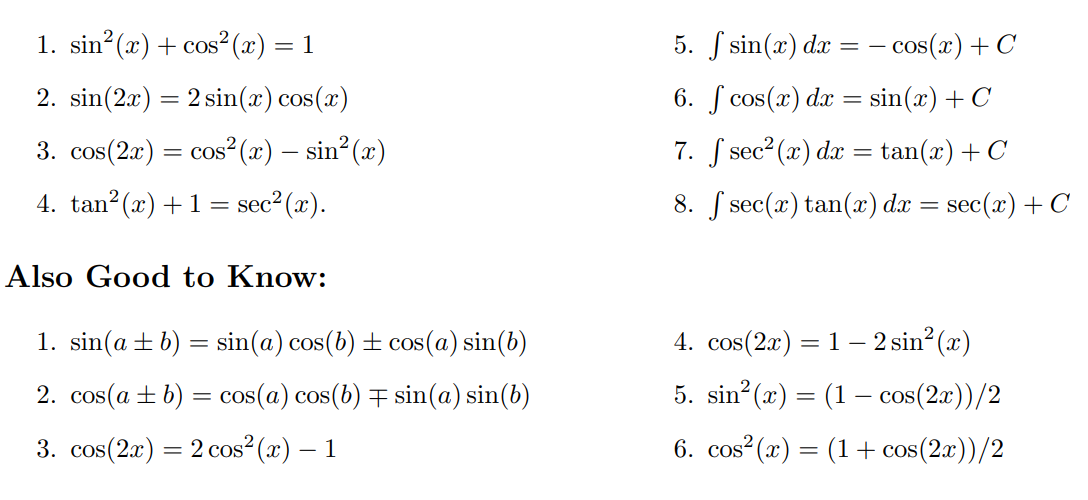
Trig Identities
- Defining relations for tangent, cotangent, secoant, and cosecant in terms of sine and cosine.

- Pythagorean formula for sines and cosines.
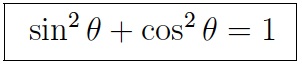
- Identities expressing trig functions in terms of their complements.

- Periodicity of trig functions.
NOTE: Sine, cosine, secant, and cosecant have period 2pi while tangent and cotangent have period pi.
- Identites for negative angles.
NOTE: Sine, tangent, cotangent, and cosecant are odd functions while cosine and secant are even functions.
- Ptolemy’s identities, the sum and difference formulas for sine and cosine.
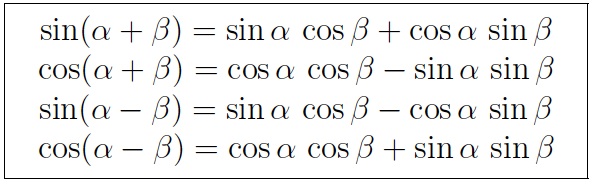
- Double angle formlas for sine and cosine
NOTE: There are three forms for double angle formula for sine.